Coordinate Systems — Cartesian and Polar

Understanding Coordinate Systems

Imagine you’re trying to describe where someone is standing in a field. You could tell them how far to the right and how far forward to walk from a fixed starting point. Or you could tell them to walk a certain distance in a specific direction. Both methods work—they’re just different ways of pinpointing the same location.

That’s exactly what coordinate systems do: they give us precise ways to describe the position of any point in a plane. In mathematics, we primarily use two main systems—Cartesian coordinates and polar coordinates—and understanding both is incredibly useful.

Two Coordinate Systems

• Cartesian coordinates: Use perpendicular distance measurements (left-right and up-down) from a fixed origin
• Polar coordinates: Use direct distance and angle measurements from a fixed origin
• Both describe the same point, just in different ways

Cartesian Coordinates

Cartesian coordinates are named after the French mathematician and philosopher René Descartes. They describe a point’s position using two numbers: how far the point is from a vertical reference line (the x-coordinate) and how far it is from a horizontal reference line (the y-coordinate).

A general pair of Cartesian coordinates is written as . For example, the point means: start at the origin, move 2 units to the right, then 7 units up.

Important note: The order matters! The point is completely different from . We call this an ordered pair because the sequence tells us which number represents the horizontal position and which represents the vertical position.

Polar Coordinates

Polar coordinates take a different approach. Instead of measuring right-and-up distances, they measure distance and direction from the origin.

A general pair of polar coordinates is written as :

• (the radius): The straight-line distance from the origin to the point, like “as the bird flies”
• (theta): The angle that this direct path makes with the positive horizontal axis, typically measured in degrees or radians

For example, the point means: start at the origin, then move 5 units away at an angle of 30° from the positive horizontal axis.

Visualizing Both Systems

The diagram below shows how these two systems represent the same point using different measurements:

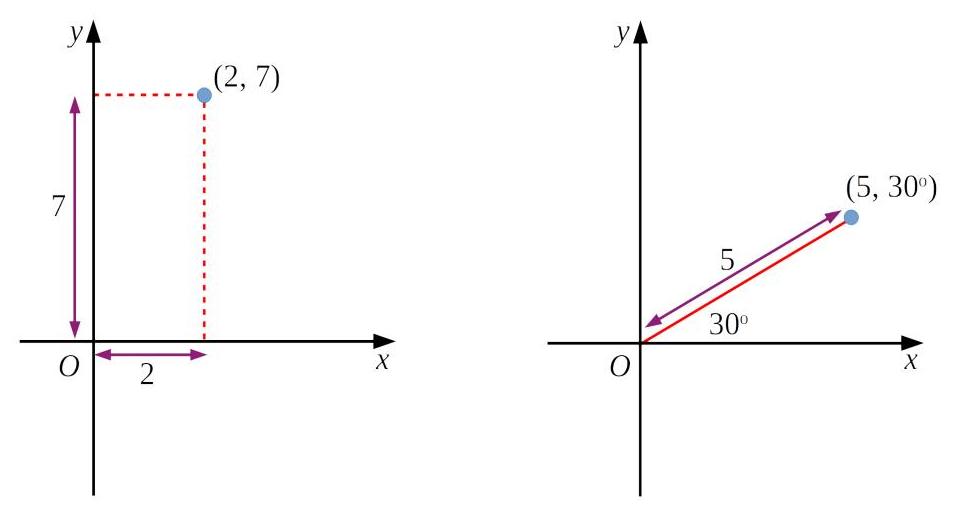
Notice how the point can be described as in Cartesian terms or as in polar terms. The visual relationship helps you see that these are truly just two different languages for describing the same location.

Converting Between Systems

Here’s where things get interesting: you can move between Cartesian and polar coordinates using basic geometry and trigonometry.

If you have a point at Cartesian coordinates , you can find the polar coordinates using the Pythagorean theorem and trigonometric ratios:

These formulas emerge naturally from right-triangle trigonometry. The distance is the hypotenuse, is one leg, is the other leg, and is the angle at the origin.

Question

How do you convert from Cartesian to polar ?

Answer

Use to find the distance, and to find the angle.

Click to flip • Press Space or Enter

Convert to Polar Coordinates

Problem

A point has Cartesian coordinates . Find its polar coordinates where is in degrees.

Show Hints (3)

Hint 1: First, find using the Pythagorean theorem:

Hint 2: Then find using inverse tangent:

Hint 3: Remember to convert radians to degrees if needed

Show Solution

Solution

First, calculate :

Then find :

So the polar coordinates are approximately .

Extending to Three Dimensions

In the real world, we don’t always work in 2D. When we need to describe points in 3D space, we have options:

• Cartesian coordinates expand to where represents height or depth
• Cylindrical coordinates combine polar coordinates in the base plane with height:
• Spherical coordinates use radius and two angles:

For the foundations we’re building here, we focus on the 2D Cartesian system, but knowing these extensions exist is important for advanced mathematics and physics.

Why Learn Both Systems?

Different problems are easier in different coordinate systems. Cartesian coordinates are great for straight lines and rectangles. Polar coordinates shine when dealing with circles, spirals, and circular motion. Learning both makes you more flexible as a problem-solver.

Key Takeaways

What You've Learned

• Cartesian coordinates describe position using perpendicular distances:
• Polar coordinates describe position using distance and angle:
• Both systems pinpoint the same location in different ways
• The conversion formulas and connect the two systems
• These concepts extend to 3D space with cylindrical and spherical coordinates

Understanding coordinate systems is fundamental to mathematics, physics, engineering, and computer graphics. You now have the foundation to recognize when each system is most useful and to convert between them as needed.