Straight Line Geometry and Perpendicular Lines

Understanding Points and Distances

When you’re working with coordinate geometry, everything starts with understanding how to measure distances between points in a plane. Let’s say you have two points: and . These are just specific locations on your coordinate grid.

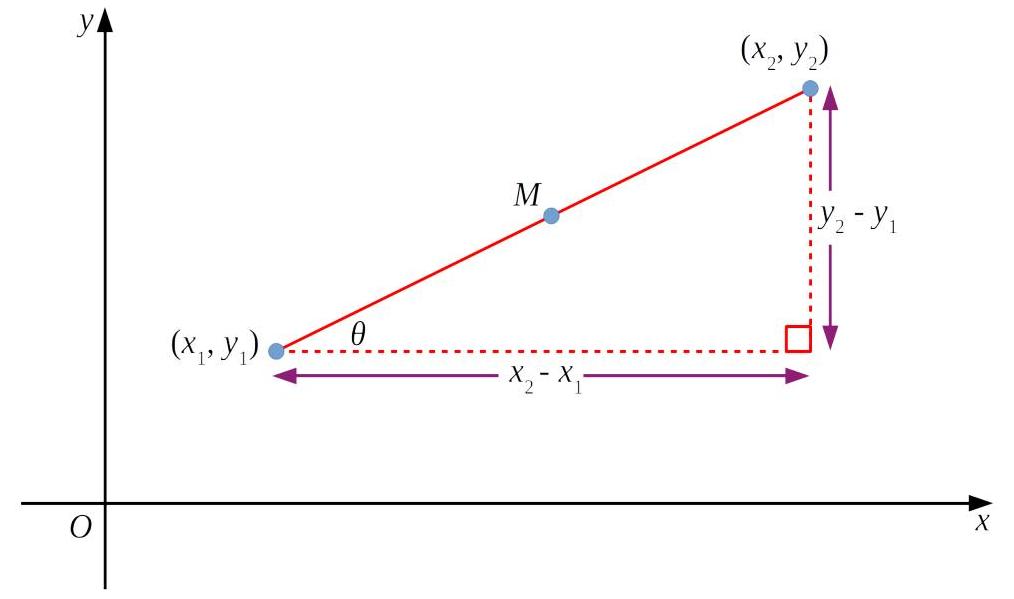
To find the straight-line distance between these points, think of it geometrically: you can move horizontally by units, then vertically by units. These two movements, along with the direct line between the points, form a right triangle. This is where Pythagoras’ theorem comes in handy.

The distance between the two points is:

Or, taking the square root:

Watch Those Negatives!

Be extra careful when coordinates involve negative numbers. The differences and can be negative, but when you square them, they become positive—exactly what you want for the distance formula.

Question

How do you find the distance between two points using the distance formula?

Answer

This comes from Pythagoras’ theorem applied to the horizontal and vertical distances.

Click to flip • Press Space or Enter

Finding the Midpoint

Sometimes you need to find the point exactly halfway between two points—that’s the midpoint. If you think about it logically, the midpoint should be at the average of the -coordinates and the average of the -coordinates.

For the -coordinate of the midpoint , we calculate:

The same logic applies to the -coordinate. So the midpoint is simply:

That’s it—just the average of each coordinate! This formula works beautifully whether your coordinates are positive or negative.

Question

What’s the midpoint formula?

Answer

Average the -coordinates and average the -coordinates.

Click to flip • Press Space or Enter

Understanding Gradient (Slope)

The gradient tells you how steep a line is—how much the line goes up (or down) as you move horizontally. The steeper the line, the larger the gradient.

If a line passes through and , the gradient is:

We often call the vertical change (delta y) and the horizontal change (delta x), so:

There’s another way to think about gradient: if the line makes an angle with the horizontal axis, then:

This connects your coordinate geometry to trigonometry—handy when you’re solving more complex problems!

Finding the Gradient

Problem

Find the gradient of the line passing through and .

Show Hints (4)

Hint 1: Remember: gradient = (change in y) ÷ (change in x)

Hint 2: Change in y =

Hint 3: Change in x =

Hint 4: Divide to find the gradient

Show Solution

Solution

The gradient is 2. For every 1 unit you move right, the line goes up 2 units.

Avoiding Division by Zero

If (the two points have the same -coordinate), then you’d be dividing by zero. This happens when the line is vertical, and we say the gradient is “undefined.”

Perpendicular Lines and the Negative Reciprocal

Here’s where things get really interesting. What happens when two lines are perpendicular (at right angles to each other)?

Imagine you have a line segment with gradient . If you rotate this segment by counterclockwise, something magical happens to the gradient.

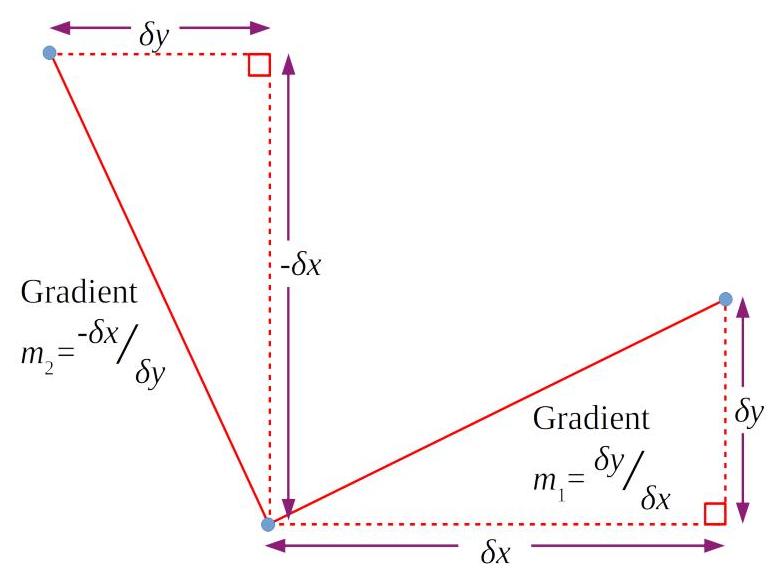
After the rotation, the new segment has gradient:

Notice what happened:

• The rise and run swapped places
• One of them got negated (changed sign)

The result is that the gradient of the perpendicular line is the negative reciprocal of the original gradient. This relationship is so important it has its own notation:

If two lines are perpendicular, their gradients multiply to give .

The Perpendicular Line Relationship

• If a line has gradient , the perpendicular line has gradient
• Equivalently:
• The negative reciprocal property is THE key to perpendicular lines
• A line with gradient 2 is perpendicular to a line with gradient
• A line with gradient is perpendicular to a line with gradient

Finding a Perpendicular Gradient

Problem

A line has gradient . What is the gradient of a line perpendicular to it?

Show Hints (3)

Hint 1: Use the negative reciprocal formula:

Hint 2: Substitute

Hint 3: Simplify the fraction

Show Solution

Solution

Any line with gradient is perpendicular to our original line.

Perpendicular Lines with Fractions

Problem

If a line has gradient , find the gradient of a perpendicular line.

Show Hints (3)

Hint 1: The perpendicular gradient is

Hint 2: Remember: (flip the fraction)

Hint 3: Don’t forget the negative sign!

Show Solution

Solution

To find the reciprocal of , flip it to get . Then add the negative sign.

Question

Two perpendicular lines have gradients and . What’s the relationship?

Answer

Or equivalently: (the negative reciprocal)

Click to flip • Press Space or Enter

Putting It All Together

Here’s a summary of the key formulas you’ve learned:

Concept	Formula	What It Tells You
Distance		Straight-line distance between two points
Midpoint		The point halfway between two points
Gradient		The slope of a line (or )
Perpendicular		When two lines are at right angles

Key Takeaways

• Distances between points come from Pythagoras’ theorem applied to horizontal and vertical distances
• Midpoints are just the averages of coordinates
• Gradient measures steepness and connects to both geometry and trigonometry
• Perpendicular lines have a special relationship: their gradients multiply to
• Always be careful with negative numbers—they’re a common source of mistakes!

Learning Checklist

Progress 0%

Congratulations! You've completed all items!

Reset Progress