The Equation of a Circle — Applications and Problems

Understanding the Circle Equation

Circles are everywhere in mathematics and the real world. Whether you’re designing a circular track, analyzing planetary orbits, or solving geometry problems, you need a way to describe a circle algebraically. That’s where the equation of a circle comes in.

Let’s start with the basics. Imagine a circle with its center at the point and a radius of . By definition, every single point on that circle is exactly the same distance from the center—that’s what makes it a circle!

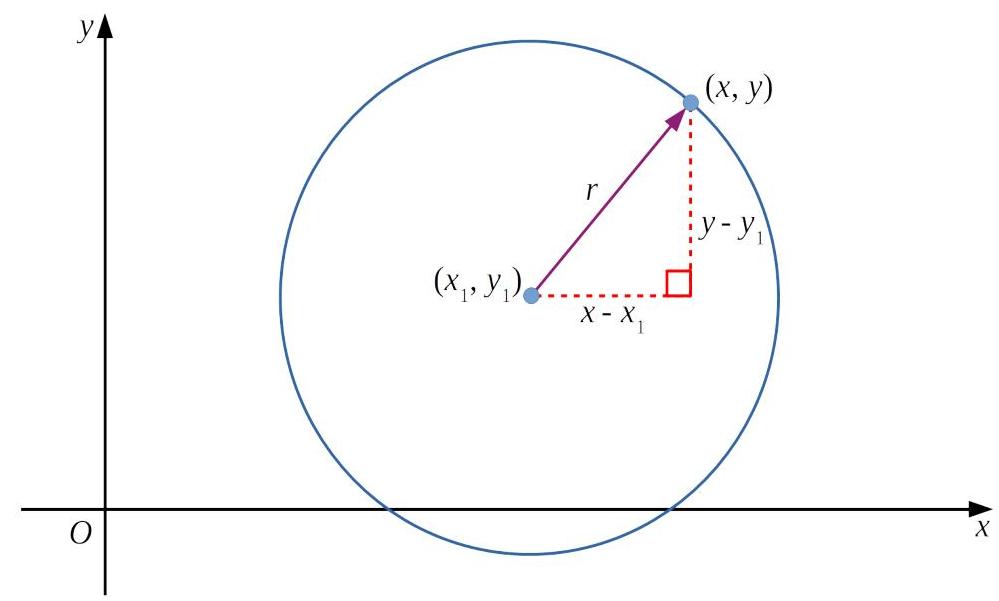
Now, consider any general point that lies on this circle. The distance from this point to the center must equal the radius . Using the distance formula—which comes straight from Pythagoras’ theorem—we get:

This is the standard form of the circle equation. It beautifully captures the defining property of a circle: all points at distance from the center .

Circle Equation Essentials

• Standard form:
• Center: is the center of the circle
• Radius: is the distance from center to any point on the circle
• Geometric meaning: Every point on the circle is equidistant from the center

Working with General Form Equations

Sometimes circle equations appear in a different form—expanded and rearranged. You might see something like . This is the general form of a circle equation, and it’s useful to convert it back to standard form by completing the square. This helps you identify the center and radius quickly.

Completing the Square

Completing the square is a powerful technique that transforms the general form into standard form, making the center and radius immediately visible.

Example: From General to Standard Form

Let’s work through a real problem. Consider the circle with equation .

To find the center and radius, we complete the square for both and terms:

From this standard form, we can immediately read off:

• Center:
• Radius: (since )

Question

What’s the standard form of a circle?

Answer

where is the center and is the radius

Click to flip • Press Space or Enter

Finding Tangent Lines to Circles

One of the most powerful applications of circle equations is finding tangent lines. A tangent line touches the circle at exactly one point and is perpendicular to the radius at that point of contact.

This perpendicularity is key! If you know the gradient of the radius, you can find the gradient of the tangent because perpendicular lines have gradients that multiply to give .

Example: Finding a Tangent Line

Let’s find the equation of the tangent to our circle at the point .

Step 1: Find the gradient of the radius from center to point of contact.

The center is at and the point of contact is at :

Step 2: Use the perpendicularity condition.

Since the tangent is perpendicular to the radius, and perpendicular gradients multiply to :

Step 3: Write the equation using point-slope form.

With gradient passing through :

So the tangent line is , or equivalently .

Circle Theorems Connection

This perpendicularity property comes from Circle Theorems—a fundamental principle stating that the tangent to a circle is always perpendicular to the radius drawn at the point of contact. It’s a beautiful result that bridges geometry and coordinate algebra!

Practice: Tangent Line

Problem

Find the equation of the tangent to the circle at the point .

Show Hints (4)

Hint 1: Identify the center of the circle:

Hint 2: Find the gradient of the radius from to

Hint 3: Use the perpendicularity condition:

Hint 4: Apply point-slope form using the point and the tangent gradient

Show Solution

Solution

Finding the radius gradient:

Finding the tangent gradient: Since , we have , so .

Finding the tangent equation:

Or in standard form:

Sketching Your Answer

A practical tip: always draw a sketch to check if your answer makes sense! Your sketch should show:

• The circle with its center clearly marked
• The point of tangency on the circle
• The radius to that point
• The tangent line perpendicular to the radius

If your sketch shows a negative gradient for the tangent but your equation gives positive, something’s wrong. Sketching catches these errors quickly and builds your geometric intuition.

Further Exploration

There’s a whole world of circle problems waiting for you:

• Touching circles: How do two circles interact? When do they touch internally or externally?
• Pairs of circles: What happens when you have multiple circles? How do you find intersection points?
• Implicit circle equations: How can we work with circles defined in more complex algebraic forms?

Key Takeaways

• The equation completely describes a circle using algebra
• Complete the square to convert general form equations to standard form
• Tangent lines are perpendicular to the radius at the point of contact
• Always sketch your answer to verify it makes geometric sense
• Circle geometry connects beautiful mathematical principles with practical applications

Question

What’s the key property of a tangent to a circle?

Answer

The tangent line is perpendicular to the radius at the point of contact. If the radius has gradient , the tangent has gradient .

Click to flip • Press Space or Enter