The Equation of a Straight Line (Derivation and Uses)

Finding the Equation of a Straight Line

The equation of a line is one of the most fundamental tools in coordinate geometry. Whether you’re analyzing a graph, solving a problem, or finding geometric relationships, knowing how to write and use the equation of a line is essential.

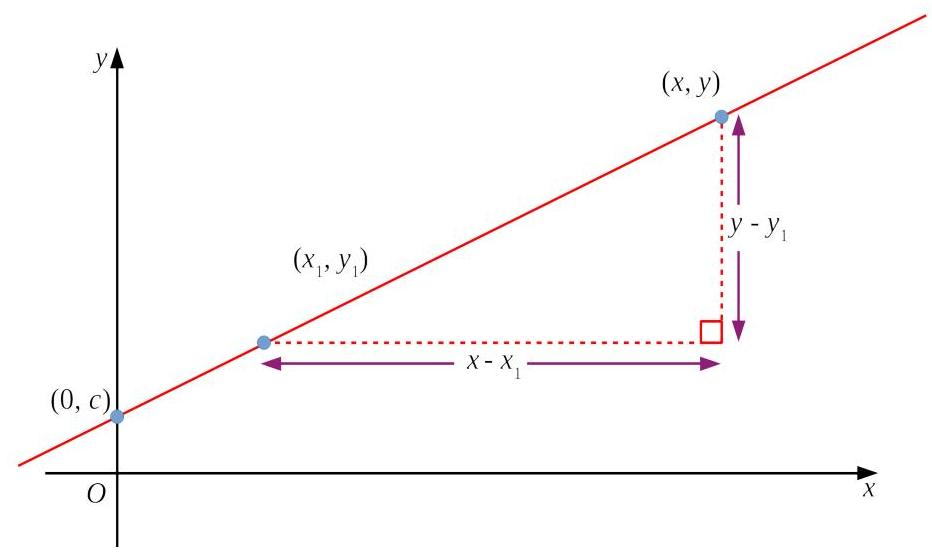
Let’s start with the core concept. Imagine a straight line with one fixed point and any variable point on that line. Since all points on a line have the same gradient, the gradient between these two points must equal the line’s gradient :

Rearranging this gives us:

Point-Gradient Form

• General form:
• What it means: Any point on the line satisfies this equation
• What we need: The gradient and any point on the line

The Slope-Intercept Form

This is probably the most familiar form. If we know the line passes through the -intercept at , we can substitute directly:

This tells us that is where the line crosses the -axis, and is the slope. This form makes it really easy to sketch a line or identify its key properties at a glance.

Finding the Equation from Two Points

Sometimes you don’t have the gradient—you just have two points the line passes through. No problem! You can:

1. Calculate the gradient using:
2. Use either point in the point-gradient form

Tip

There’s a formula that combines both steps: . But honestly, it’s easier to calculate the gradient first, then use the point-gradient form!

Working Example: Finding the Circumcentre

Let’s work through a complete problem that ties together everything we’ve learned. This is the kind of problem that shows why the equation of a line is so powerful.

Problem: A triangle has vertices at , , and .

• (i) Find the perpendicular bisectors of and
• (ii) Find where these two lines intersect
• (iii) Find the perpendicular bisector of and verify all three meet at the same point

Strategy: Always sketch the three points roughly in the correct positions first. Your sketch helps you check if your answers make sense.

Part (i): Finding the Perpendicular Bisectors

For a perpendicular bisector, we need:

1. The midpoint of the line segment
2. A gradient perpendicular to the original segment (negative reciprocal)

Perpendicular bisector of AB:

• Midpoint of and :
• Gradient of :
• Perpendicular gradient: (negative reciprocal of )
• Using point-gradient form with :

Perpendicular bisector of BC:

• Midpoint of and :
• Gradient of :
• Perpendicular gradient: (negative reciprocal of )
• Using point-gradient form with :

Part (ii): Finding the Intersection

Now we solve these equations simultaneously to find where the two perpendicular bisectors meet:

The two perpendicular bisectors intersect at .

Part (iii): Verifying the Third Bisector

Let’s find the perpendicular bisector of and check that it also passes through our intersection point.

Perpendicular bisector of AC:

• Midpoint of and :
• Gradient of :
• Perpendicular gradient: (negative reciprocal of )
• Using point-gradient form with :

Verification: Substitute into this equation:

Perfect! The point lies on all three perpendicular bisectors, confirming they meet at a single point.

The Circumcentre

• The three perpendicular bisectors of a triangle’s sides always meet at one point called the circumcentre
• You can draw a circle through all three vertices (the circumcircle) with the circumcentre as its center
• This elegant property shows how the line equations connect geometry in beautiful ways

Key Techniques to Remember

Question

What is the point-gradient form of a line equation?

Answer

where is the gradient and is any point on the line

Click to flip • Press Space or Enter

Question

What is the slope-intercept form?

Answer

where is the gradient and is the -intercept

Click to flip • Press Space or Enter

Question

How do you find the gradient of a perpendicular line?

Answer

Take the negative reciprocal. If the original line has gradient , the perpendicular line has gradient

Click to flip • Press Space or Enter

Practice: Finding a Line Equation

Problem

A line passes through the points and . Find the equation of this line in the form .

Show Hints (3)

Hint 1: First, find the gradient using the two points

Hint 2: Then use the point-gradient form with either point

Hint 3: Finally, rearrange to get

Show Solution

Solution

Step 1: Calculate the gradient:

Step 2: Use point-gradient form with :

Step 3: Rearrange: , so

The equation is

Challenge: Perpendicular Bisector

Problem

Find the equation of the perpendicular bisector of the line segment from to .

Show Hints (4)

Hint 1: Find the midpoint of

Hint 2: Find the gradient of

Hint 3: Find the perpendicular gradient

Hint 4: Use point-gradient form with the midpoint

Show Solution

Solution

Step 1: Midpoint:

Step 2: Gradient of :

Step 3: Perpendicular gradient:

Step 4: Using :

Result: or equivalently

Putting It All Together

The equation of a line is far more than just a formula to memorize. It’s a bridge between algebra and geometry, allowing you to describe positions, relationships, and patterns. Whether you’re finding where two lines cross, constructing perpendicular bisectors, or analyzing geometric properties like the circumcentre, you’re using the same fundamental principles.

Master these forms and you’ll find coordinate geometry becomes much more intuitive:

• Point-gradient form () for when you know a point and the slope
• Slope-intercept form () for when you know the intercepts and slope
• Perpendicular relationships (gradient perpendicular gradient = ) for geometric constructions

Now you’re ready to tackle more complex coordinate geometry problems!